Say you are developing a game like Chess, Go, Checkers, Tic-Tac-Toe or Memory. In each of those games the game board is a rectangle looking playfield of different size (rows x columns). Tic-Tac-Toe is 3×3, Checkers is 8×8, while Go can be 19×19 or 13×13 and similar.

In a game with an arbitrary number of game fields you might want to have the board look as closely to square as possible (rectangle where height and width are the same). Think of Memory. Let’s say we have 24 cards, that is 12 pairs. If you want to place them in a rectangular grid, most similar to square, you would go for 4 x 6 (or 6 x 4) board size (as it would look more square like than 3 x 8 and 2 x 12 or 1 x 24 would be too wide).

Therefore, the question: having an arbitrary number of game field pairs, what is the ideal, most square looking, grid size?

And the answer is an algorithm (some math knowledge required) like this one:

TGridSize = record
  Rows, Columns : integer;
end;

function CalcGridSize(const numberOfPairs : Cardinal) : TGridSize;
//look for ideal rectangle dimensions (square is ideal)
//to present fields, number of fields = 2 * numberOfPairs
var
  fieldCount : integer;
  i : integer;
begin
  fieldCount := 2 * numberOfPairs;

  result.Rows := 1;
  result.Columns := fieldCount;

  if Sqrt(fieldCount) = Trunc(Sqrt(fieldCount)) then
  begin
    result.Rows := Trunc(Sqrt(fieldCount));
    result.Columns := Trunc(Sqrt(fieldCount));
    Exit;
  end;

  for i := Trunc(Sqrt(fieldCount)) downto 2 do
    if (fieldCount mod i) = 0 then
    begin
      result.Rows := i;
      result.Columns := fieldCount div i;
      Exit;
    end;
end; (*CalcGridSize*)

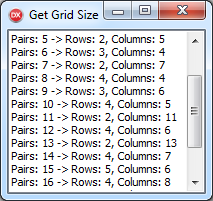
And here are some results:

var
  gridSize : TGridSize;
  i : integer;
begin
  for i := 1 to 20 do
  begin
    gridSize := CalcGridSize(i);
    ListBox1.Items.Add(
      Format('Pairs: %d -> Rows: %d, Columns: %d', 
             [i, gridSize.Rows, gridSize.Columns]));
  end;
end;

Ideally, if we have (for example) 8 pairs, that is 16 fields, the grid size is 4×4 as the square root of 16 is 4.
For 10 pairs, 20 fields, the size would be 4×5.

In worst case scenarios, where the number of pairs is a primary number (dividable only by 1 or itself), the grid will always calculate to 2 x numberOfPairs. Here you might want to add another parameter to the function – something like how many dummy/non-playable fields to add to the grid so it looks more square like. I’ll leave this to you.

That’s it. If you have a better (faster, more elegant) solution, I’d certainly love to see it…